a) environment 1 |

b) environment 2 |
c) environment 3 |
Chaiwat Jassadapakorn and Prabhas Chongstitvatana
Intelligent
System Laboratory
Department
of Computer Engineering
Chulalongkorn
University
Phayathai Road, Bangkok 10330, Thailand
prabhas@chula.ac.th
Abstract
There are many methods to reduce computational effort when using Genetic Programming to solve problems. The Automatic Defined Function (ADF) is a well known method. In ADF, an individual is composed of a main routine and subroutines. The number of subroutines is determined before the run. The efficiency depends on choosing a suitable number of subroutine for the problem. This work proposed an extension of ADF, called ADFX, where the number of subroutines is determined as a range. ADFX is easier to use. The result of the experiment shows that ADFX reduces the computational effort and compares favorably with ADF.
1. Introduction
Genetic Programming (GP) is a technique for machine learning which is developed from Genetic Algorithm [1]. It is inspired by natural selection and genetic operations in biology. GP technique is suitable for solving a wide variety of problems but the requirement of computational effort is high. There are many works which try to increase the efficiency of GP.
Module acquisition (MA) [2] and Automatically Defined Function (ADF) [3] are two well known techniques to increase the efficiency of GP. MA uses the concept of modular programs, an individual can refer to subroutines in the library which are acquired from parts of randomly selected individuals. A subroutine will remain in the library until there is no individual call it. The chance of being called is increased according to its usefulness measured by its fitness value.
An individual in ADF has a structure that composed of a main routine and subroutines. In contrast to MA, subroutines in ADF will no be shared amongst individuals. In order to use ADF, some parameters have to be determined : the number of subroutines and the number of arguments of each subroutine. When there are more than one subroutine, the hierarchy of subroutine calls has to be established. Choosing these parameters is an important part of ADF technique. It depends on the problem being solved. The incorrect choice of parameters will decrease the efficiency of GP.
This work describes an extension of ADF technique, called ADFX. The aim is to improve the flexibility in choosing the number of subroutines while retains the good efficiency of ADF. The next section explains and defines the computation effort. The section 3 details the ADFX technique and the section 4 describes a case study of using ADFX to solve the problem of controlling a robot arm. In the section 5, the process of GP to solve this problem is explained. The section 6 discusses the result of the experiment, the related work is presented in the section 7 and the resultant conclusion is given in the section 8.
2. Computational Effort
The measurement of efficiency of GP process is done using statistical approach because GP process employs randomization. The result of the experiment varies from one run to another run. The computational effort is calculated from the data gathered from many runs. Computational effort is defined as the minimum number of individual that must be processed to get the answer. The definition of computational effort is proposed by Koza [3].
Let P(M,i,z) be the probability of finding the answer within the generation i, M is the number of individual in the population. P can be observed by repeating the experiment many times. R(M,i,z) be the number of run required to find an answer in the generation i with the confidence z. R(M,i,z) = ceiling( log(1-z)/ log(1- P(M,i,z)) ). The minimum number of individual that must be processed to find an answer with the confidence z is I(M,i,z) = M ´ i ´ R(M,i,z). The minimum value of I(M,i,z) is defined as the computation effort. The confidence z in this work is 99 %.
3. Extension of Automatic Defined Function
In using ADF, the number of subroutines is important. The knowledge about the problem is required to determine the suitable number of subroutines to solve that problem efficiently. An extension of ADF, called ADFX is proposed as follows :
1. Determine the number of subroutines as a range
This allows the flexibility in determining of the number of subroutines. Initial population is created with an individual that has a number of subroutine within the determined range. This results in a population that each individual has a different number of subroutines. The successful individual will be propagated to the next generation. Therefore a suitable number of subroutines will be automatically emerged.
2. Allow the crossover operation between different subroutines
The crossover operation in ADF is between the same kind of subroutine, i.e. the ADF with the same numbering. Because in ADFX each individual has different number of subroutines therefore it must be possible for different subroutines to crossover. This increases the possibility of combining the good subroutines together. There are problems when allowing crossingover of different subroutines. One is that of referencing to the non-exist subroutine. Another is in breaking the hierarchy rule. These problems are solved by interpreting such erroneous calls as no operation (NOP).
4. Case study : Controlling a manipulator
The problem of controlling a manipulator to reach a target is taken from [4,5]. GP is used to generate robot programs to control a robot manipulator to reach a target while avoiding obstacles. In this paper we use to term "individual" to mean "robot program" for this problem.
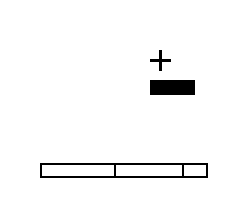
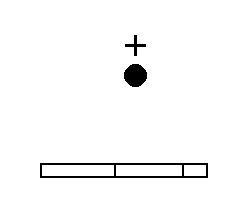
The robot system composed of a 3 DOF manipulator and a vision system mounted above and overlooking the whole work space. The vision system monitors the positions of various objects : the manipulator, the obstacles and the target. Data from the real world is sampling and uses in the simulated world in which GP is operated. GP generates robot programs that can control the manipulator. The manipulator is a 3 links planar arm moving on a plane. Movement of each joint is limited.
The environment for the experiment
is shown in the figure below : (solid blocks is obstacles and a cross is
the target)

a) environment 1 |

b) environment 2 |

c) environment 3 |
5. Genetic Programming Process
5.1 Parameters in ADF and ADFX
1 the number of arguments
: It is set of zero to reduce the number of experiment. If we consider
each instantiation of arguments in a subroutine as a different subroutine,
we can reason that subroutines with no argument are similar to different
subroutines with instantiation of arguments.
2 the number of subroutines
: It is varied from 1-16 for ADF and for ADFX the range is varied from
0-1 to 0-16 subroutines.
3 the reference between subroutines
: Hierarchical rule is implemented. The main routine can call any subroutine.
The higher number subroutine can call the lower number subroutine.
5.2 Robot program structure
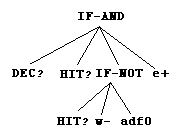
Each program is composed of main routine and subroutines. It has a tree structure composed of symbols from the function set and the terminal set.
function set = { IF-AND, IF-OR, IF-NOT
}
terminal set = { s+, s-, e+, e-,
w+, w-, HIT?, SEE?, INC?, DEC?, OUT?, adf0...adf15 }
The function s+ (shoulder) drives
the shoulder motor clockwise 1 step (5 degrees) and s- drives the shoulder
motor anticlockwise 1 step. The similar meaning applies for e+, e- (elbow)
and w+, w- (wrist). All of these functions always return true. The function
HIT? checks whether each link of the robot arm hits the obstacle. The function
SEE? checks whether the path from the fingertip to the goal has any obstacle.
The function INC? checks whether the distance between the fingertip and
the goal is increasing. The function DEC? checks the opposite. The function
OUT? checks if each joint of the robot arm moves out of bound. The bound
is defined to prevent the arm from going out of the view of the camera.
The function IF-AND is a four-argument comparative branching operator that
executes its third argument if its first argument and its second argument
are true, or otherwise, executes the fourth argument. The function IF-OR
is a four-argument operator that executes its third argument if its first
argument or its second argument is true, or otherwise, executes the fourth
argument. The function IF-NOT is a three-argument operator that executes
its second argument if the negation of its first argument is true, or otherwise,
executes the third argument. The function adf0...adf15 is the call to subroutines.
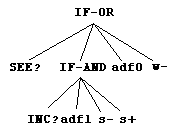 |
 |
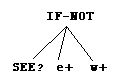 |
| Main routine | Subroutine ADF1 | Subroutine ADF0 |
5.3 Genetic operations
We use four genetic operations :
reproduction, crossover and two kinds of mutation. Addition is the mutation
by attaching a newly generated tree of height 1 at the root of a tree.
Extension is similar but attached at the leaf node (fig. 3).
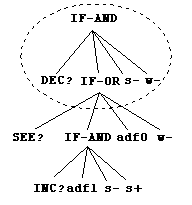 |
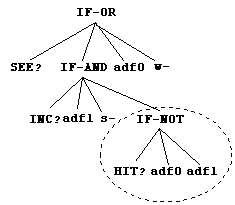 |
| a) Addition | b) Extension |
5.4 Fitness evaluation
The fitness of individual program is evaluated with the following function :
- 2000 x finalDistance / initialDistance - 100 x finalDistance / sumDistance - 1000 x notSee - 4000 x die
where initialDistance is the initial distance from the fingertip to the target, finalDistance is the distance from the fingertip to the target after the program execution is terminated, sumDistance is the total of distance that the fingertip travelled, notSee is a Boolean variable that indicate the path from the fingertip to the target is blocked by an obstacle, and die is a Boolean variable that indicate the dead condition. For a full account of the experimental setup please refer to the original papers [4, 5].
This function indicates that the better program has a higher fitness value by getting closer to the target, using shorter path and at the end of the run the tip of the manipulator reaches an opening.
5.5 Parameters of GP run
Parameters are shown in the table 1.
Table 1 Parameters of the GP run
| population | 400 programs |
| initial size of an individual | 80 symbols |
| maximum generation | 10 |
| number of repeated run | 1000 runs |
| reproduction rate | 10 % |
| crossover rate | 40 % |
| addition rate | 25 % |
| extension rate | 25 % |
6. Results
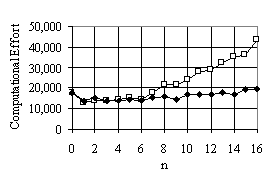
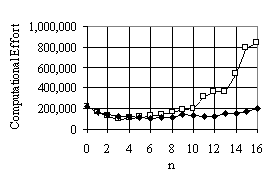
We compare the computational effort between the run without ADF, with ADF and with ADFX. The results of three experiments are shown in the table 2 and figure 4. The best result from ADF has lower computational effort than without ADF in the environment 1 and 2 and has significantly lower computational effort in the environment 3 (which is the most difficult problem). This shows that ADF can increase the efficiency of GP for the robot problems. The more difficult problem shows the higher benefit. The number of subroutines has impact on the efficiency. The suitable number for this problem is 1-3 subroutines. When the number of subroutines is increase beyond 3 the efficiency is declined. The worst case is the maximum number of subroutines (16) in which the computational effort is much higher than the run without ADF.
In comparing ADFX to ADF, the best result of ADFX for each environment has slightly higher computational effort than the best result of ADF. But in the worst case, ADFX has a much better behaviour than ADF when the number of subroutines varies from 0-16. We conclude that ADFX is similar in efficiency to ADF when ADF has a suitable number of subroutines. Although the best case of ADFX is slightly worse than the best case of ADF, ADFX performs well without having to determine a priori the number of subroutines. A more detail of the experiment with different environments can be found in the master degree thesis [6].
Table 2 Computational effort of the experiment
|
|
|
|
|
||
|
|
|
|
|
||
|
|
14,400
|
12,800
|
43,200
|
12,800
|
24,000
|
|
|
18,000
|
12,800
|
43,200
|
14,000
|
19,600
|
|
|
220,800
|
99,200
|
834,000
|
104,000
|
201,600
|
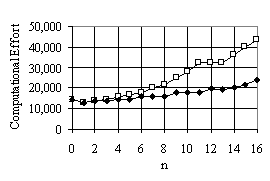
a) environment 1 |
b) environment 2 |
c) environment 3 |
![]() ADF n function(s)
ADF n function(s) ![]() ADFX 0-n
function(s)
ADFX 0-n
function(s)
Figure 4 Comparing computational effort of ADF and ADFX
7. Related work
The method of ADFX proposed here
is similar to another extension of ADF, called ADF with evolution of architecture
(EADF) by Koza [3]. In EADF the number of subroutines and the number of
arguments is randomly chosen for each individual. The crossover in EADF
uses "point typing" to solve the problem of crossing between different
subroutines whereas ADFX has no such restriction. Point typing preserves
the structure of subroutines and restricts hierarchy of subroutine calls.
ADFX is different from EADF in the crossover operation where ADFX allows
any subroutine to cross with any subroutine without restriction. We have
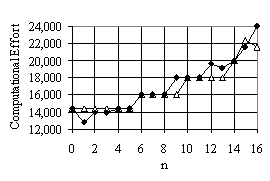
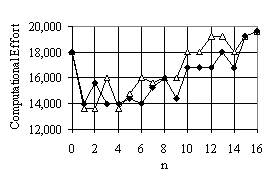
compared EADF with ADFX for the robot problem. The result is shown in fig.
5. Our conclusion is that ADFX and EADF have similar efficiency.
a) environment 1 |
b) environment 2 |
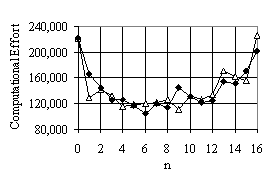
c) environment 3 |
![]() EADF n function(s)
EADF n function(s) ![]() ADFX 0-n
function(s)
ADFX 0-n
function(s)
Figure 5 Comparing computational effort of ADFX and EADF
8. Conclusion
This paper describes ADFX which is an extension of ADF with two improvements : the number of subroutines is determined as a range and allows crossover between different subroutines. The result of experiment shows that ADFX reduces computational effort significantly compared to a method without ADF. ADFX has an advantage over ADF that the exact number of subroutines, which affects the computational effort, is not required a priori. For the problem which the suitable number of subroutines in not known, ADFX is a good choice for reducing computational effort.
References
| [1] | Holland, J., Adaptation in Natural and Artificial System, Ann Arbor, Michigan : University of Michigan Press, 1975. |
| [2] | Angeline, P., "Genetic Programming and Emergent Intelligence", In K. E. Kinnear, Jr. (ed.), Advances in Genetic Programming, pp. 75-98, MIT Press, 1994. |
| [3] | Koza, J. Genetic Programming II: Automatic Discovery of Reuseable Programs, MIT Press, 1994. |
| [4] | Polvichai, J., "Robot Learning by Genetic Programming", Master's Thesis, Department of Computer Engineering, Chulalongkorn University, 1996. (In Thai) |
| [5] | Chongstitvatana, P. and Polvichai, J., "Learning a Visual Task by Genetic Programming", Proc. of the 1996 IEEE/RSJ Int. Conf. on Intelligent Robots and System, Osaka, Japan, pp. 534-540, 1996. |
| [6] | Jassadapakorn, C., "Reduction of Computational Effort in Genetic Programming Learning Method", Master's Thesis, Department of Computer Engineering, Chulalongkorn University, 1997. (In Thai) |