In this note, I will introduce you to start writing a program in recursive style. All examples here can be written in C using my list library here.
A list contains varying numbers of different objects, for example number (integer) and string (name). A simple object is called an atom. A list can contain another list. Here is a list.
(1 3 "hello") ( (3 4) ("a" "b" "c") )
Many kind of objects can be represented by lists. For example an
expression:
a = b + c
can be drawn as a tree where the root is an operator like this,
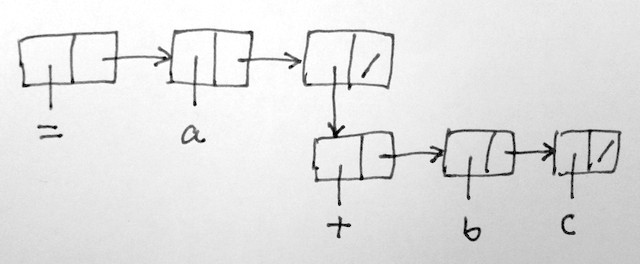
head(L) returns first element of the listtail(L) returns the list without the first elementcons(X,L) returns a new list with X as its head and L as its
tail.L is cons( head(L), tail(L) )number(n) returns an atom of number nstring(s) returns an atom of string sisatom(X) checks if X is an atom (1 2) is cons(number(1), cons(number(2), NIL))Now that we know list, let us start by writing a simple program to count the number of elements in a list. We will start with a simple iterative version using "while".
Let input be a list of numbers such as (1 2 3 4)
count1(L)
s = 0
while L != NIL
L = tail(L)
s++
return s
The iteration works as L is shortening until it is empty. Instead of using "while", we can do a recursion on tail(L).
count2(L)
1. if L == NIL return 0
2. return 1 + count2(tail(L))
The recursion on Line 2 continue on the tail(L). Line 1 tells us when to stop. The result is pending 1 + 1 + ... 0 until L is empty on the last call and return 0, then all the 1 + 1 + ..0 are executed and return. Let us see how the list L behaves.
count2( (1 2 3) )
1 + count2( (2 3 ) )
1 + count2( (3) )
1 + count2( NIL )
0
Now count1 and count2 give the same result. count2 is a recursive version. However count2 will not count "inside" the element which is a list, for example count2 ( (1 (2 3)) ) returns 2 instead of 3. We will refine it to do that.
count3(L)
1. if L == NIL return 0
2. if isatom(head(L)) return 1 + count3(tail(L))
3. ... if head(L) is a list, what to do?
The count3 is similar to count2. Line 2 of count3 is modified from Line 2 of count2 but now it checks that the current element is not a list. So, what to do if it is a list? Let us consider what count3 is written to do. It can count "inside" a list. If we assume for now that it can do that, then we can use count3 to work in Line 3.
count3(L)
1. if L == NIL return 0
2. if isatom(head(L)) return 1 + count3(tail(L))
3. return count3(head(L)) + count3(tail(L))
So, Line 3 is where the magic occurs. When you think of it, if head(L) is an atom, Line 3 will be reduce to 1 + count3(tail(L)) which is exactly like Line 2 of count2. Let us try count3 on (1 (2 3) )
count3( (1 (2 3) ) )We can refine count3 a bit further. Noticing that Line 2 can be simplified.
count3(L)
1. if L == NIL return 0
2. if isatom(L) return 1
3. return count4(head(L)) + count4(tail(L))
We have learn how to write a recursive program to take apart a complex structure. Next exercise is to "build" a recursive structure. Let us start with building a unary number which is represented by a list of 1's. Given a number n, write a program to produce a list of n 1's. (1 1 ...). As before we will start with an iterative version.
unum1(n)
L = NIL
while n > 0
L = cons(number(1),L)
n--
return L
We use iteration to cons' "1" into a list, n times.
unum1(2) returns (1 1)
unum1(3) returns (1 1 1)
A recursive version use the recursion of reducing n until it is 0.
unum2(n)
1. if n == 0 return NIL
2. return cons(number(1), unum2(n-1))
Line 2 did exactly that. The cons' of 1 is pending while unum2 keeps producing the next 1 ... until n == 0.
unum2(3)
cons(1, unum2(2))
cons(1, unum2(1))
cons(1, unum2(0))
NILreturn cons(1, cons(1, cons(1, NIL ))) == (1 1 1)
Let try to define some arithmetic operation on this unary number. Starting with add.
(1 1) + (1 1 1) = (1 1 1 1 1) that is 2 + 3 = 5
So, adding two unary numbers is just merging two lists. We start by trying to write a concatenate function for two lists. We will take one element from the fist list and "cons" it to the second list. An iterative version is this.
cat1(a b)
1. while a != NIL
2. b = cons(head(a), b)
3. a = tail(a)
return b
Now we can try a recursive version.
cat2(a b)
1. if a == NIL return b
2. return cat2( tail(a), cons(head(a),b) )
Line 2 of cat2 did the work similar to Line 2,3 of cat1. Building up a result is done by "cons". Reducing a (hence converge to a stop in the end) is done by tail(a). However please observe the order of "cons". For illustration, we will use lists of integer.
cat2( (1 2) (3 4 5) )
cat2( (2) (1 3 4 5) )
cat2( NIL (2 1 3 4 5) )
Fortunately, for unary addition, the order is not relevant. So, uadd(a b ) == cat2(a b). We can refine it a bit more by recognising an arithmetic identity.
n + 0 = n, 0 + m = m
uadd(n m)
if m == NIL return n
if n == NIL return m
return uadd( tail(n), cons(head(n),m))
To complete the arithmetic operation, let we try a subtraction. We notice that we can take an element away from both number one-by-one until one list is empty. The remaining list is the difference. Let assume n >= m, so m will be empty first.
usub(n m) we assume n >= m
if m == NIL return n
return usub( tail(n), tail(m) )
It turns out that subtraction is easier than addition in this unary system. (In tenary number, subtraction is more difficult than addition).
There is one more thing I want to tell you. When you want to build up a result, you can use an additional variable to hold it. This variable is usually passed as an extra parameter to your recursive function. Let me give an example of reversing a list. Write a program to reverse a list, returning a new reversed copy of the original. Where will you keep the result in progress?
reverse(L)
but if you have an extra parameter, you can keep your intermediate result there.
reverse2(L, L1)
if L == NIL return L1
return reverse2( tail(L), cons(head(L), L1)
Now you can write your reverse. The "accumulating" variable starts with NIL. Did you notice that reverse2 is like cat2? (Think why?)
reverse(L)
return reverse2(L, NIL)
I will show how to represent a program with List. Use count_simple(L) as
a case study.
We will represent a statement by a list with the first element as
"operator" and the rest of the list are the arguments to that operation.
( op arg1 arg2 ... )
to define a function we will use the operator "def". So, to define
count_simple(L):
program -> ( "def" "count_simple" arglist body )
arglist -> ( "L" )
the body of this function consists of two lines.
line1 -> ("if" ( "==" "L" nil) ("ret" 0))
line2 -> ("ret" ("+" 1 ("count_simple" ("tail" "L")))
nil is a special atom is our universe of objects. To represent a "block"
of statement we use the operator "do".
body -> ("do" line1 line2)
("def" "count_simple" ("L")
("do"
("if" ("==" "L" nil) ( "ret" 0))
("ret" ("+" 1 ("count_simple" ("tail" "L"))))) (+ 1 2).
The needed operators are (if cond true-act false-act) for
if..then..else and (do ex1 ex2) for executing ex1 follows by
ex2. Defining a function will be a bit tricky, you need to be able to create
a variable (called lambda in programming language theory). An example of
this language (of the above reverse2 definition):(def reverse2 (L L1) (if (eq L NIL) (L1) (reverse2 (tail L)
(cons (head L) L1))))No you don't need to fire up your compiler. You can write all of them down in a sheet of paper. How can you know that you got it right? Simply, prove it :-)
But if you want to try to run it, you can code it in C. Here is the C program of the above examples. This program is used in conjunction with the ailib.c, ailib.h library.
a cell has two fields: head, tail. notation [head : tail]
we use cells to store two kinds of things: list, atom
1) list
a list is a linked list. head points to "value" which is atom or another list. tail points to another cell. list ends with tail equals NIL.
[ : ] -> [ : ] -> ... [ : NIL][type : value]
cells[.] are array of cell. It is divided into two parts. list and atom
are allocated from different parts of cells[.]. atoms are allocated from
the "lower" part and lists are allocated from the "upper" part. ATOMTYPE
is the divide line between lower and upper part. The total number of atom
in the system determines where to set ATOMTYPE.
We can distinguish atom and list by looking at its pointer (an index).
if idx < ATOMTYPE it is an atom
else it is a list
cells
[ ... [ : ] [ : ] ...]
atoms ^ lists
|
ATOMTYPE
example 1: list of number. (1 2 3)
1000 [10 : 1002], 1002 [12 : 1004], 1004 [14 : NIL]
10 [number : 1]
12 [number : 2]
14 [number : 3]
example 2: list of name. ("a" "b")
2000 [20 : 2002], 2002 [22 : NIL]
20 [name : 0]
22 [name : 2]
string table
index 0 2
["a", "b" ...]
example 3: complex list. ("a" (1 2))
3000 [30 : 3002], 3002 [3010 : NIL]
3010 [32 : 3012], 3012 [34 : NIL]
30 [name : 0]
32 [number : 1]
34 [number : 2]
string table
index 0 2
["a", "b" ...]
last update 7 April 2022