Modern Genetic Algorithms
Prabhas Chongstitvatana
Department of computer engineering
Chulalongkorn university
National Computer Science and Engineering Conference 2004
Outline
Introduction to GA
Simple Genetic Algorithm
GA versus Others
What problem GA is good for?
Applications
Theory of GA (Schema theorem)
Modern GA
Probabilistic model-building GA
Probability vector
Extended compact GA
Bayesian Optimisation Algorithm (BOA)
Simulaneity matrix
Conclusion
Genetic Algorithms
A class of probabilistic search, inspired by natural evolution.
"the fittest survives"
GA works on a set of solution, called "population".
GA uses fitness function to guide the search.
GA improves solutions by genetic operators:
selection
recombination (crossover)
mutation
GA pseudo code
initialise population P
while not terminate
evaluate P by fitness function
P' = selection.recombination.mutation of P
P = P'
terminating conditions:
1 found satisfactory solutions
2 waiting too long
Simple Genetic Algorithm
represent a solution by a binary string {0,1}*
selection:
chance to be selected is proportional to its fitness
recombination
single point crossover
recombination
select a cut point cut two parents, exchange parts
AAAAAA 111111
AA AAAA 11 1111
cut at bit 2AA1111 11AAAA
exchange partsmutation
single bit flip
111111 --> 111011 flip at bit 4
GA compare to other methods
"
indirect" -- setting derivatives to 0"direct" -- hill climber
enumerative search them all
random just keep trying
simulated annealing single-point method
Tabu search
What problem GA is good for?
Highly multimodal functions
Discrete or discontinuous functions
High-dimensionality functions, including many
combinatorial ones
Nonlinear dependencies on parameters
(interactions among parameters) -- "epistasis"
makes it hard for others
Often used for approximating solutions to NPcomplete
combinatorial problems
Applications
optimisation problems
combinatorial problems
binpacking 3D (container loading)

representation
1352689......
fitness function:
num. of bin + empty space in the last bin
evolve robot programs for a biped

<video of biped walking>
representation
mn....
m = {0+,0-,1+,1-,....6+,6-}
n is num. of repeat
fitness function:
six stages of walking
Evolve a leafs form

Why GA work?
Schema theorem
schema represents set of individual
{0,1,*} * = any
1******
**0**
1*****1
schema compete with each other and go through genetic operations
How many schema are there?
2
GA sampling schema in parallel and search for solutions (implicit parallelism) O(n
3) n is population sizeSimple Genetic Algorithm Analysis
m(H,t)
num. of schema H at time treproduction
m(H,t+1) = m(H,t) f(H)/f'
![]()
f'
= average fitnessm(H,t+1) = m(H,0) (1+c)
twhere c is the portion of schema that is has its fitness above average
recombination
Let
p survival probability
pc crossover probability
d(H) defining length
l length of individual
p ≥ 1 - pc d(H)/(l-1)
m(H,t+1) ≥
m(H,t) f(H)/f' [ 1 - pc d(H)/(l-1) ]
mutation
Let
pm a single position mutation probability
o(H) order of schema
probability of surviving mutation
(1 - pm)
o(H)pm << 1, approx.
1 - o(H) pm
conclusion
m(H,t+1) ≥
m(H,t) f(H)/f'[1 - pc d(H)/(l-1)- o(H)pm ]
short, low order, above average, schema grows exponentially.
Building Block Hypothesis
BBs are sampled, recombined, form higher fitness individual.
"construct better individual from the best partial solution of past samples." (Goldberg 1989)
Probabilistic model-building GA
(Estimation of distribution algorithms)
GA + Machine learning
current population
-> selection -> model-building -> next generationreplace crossover + mutation with learning and sampling probabilistic model
simple example
probability vectorp = (p1, p2, .. pn)
pi = prob. of 1 in position i
learn p: compute proportion of 1 in each position
sample p: sample 1 in position i with prob. pi
|
11001 10101 |
1.0, 0.5, 0.5, 0.0, 1.0 |
10101 10001 11101 11001 |
<ppt GECCO page 3-5>
PBIL (Baluja, 1995)
Compact GA (Harik, Lobo, Goldberg, 1998)
UMDA (Muhlenbein, Paass, 1996)
improvement
consider n-bit statistics instead of 1-bit
How to learn and use context for each position?
Then, we could solve problems decomposable into
statistics of order at most k with O(n
2) evaluations.
Extended compact GA (Harik, 1999)
model
ABCDEF
AB C DEF
00 16% 0 86% 000 17%
01 45% 1 14% 001 2%
10 35% . . .
11 4% 111 24%
iterative merge two groups
metrics: minimum description length
minimise num. of bits to store model+data
MDL(M,D) = D_model + D_data
D_data = - N
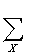 p(X) log p(X)
p(X) log p(X)
D_model =
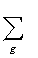 2(g-1) log N
2(g-1) log N
Bayesian Optimisation Algorithm (BOA)
(Pelikan, Goldberg, Cantu-paz, 1998)
Bayesian network as a model
acyclic directed graph
nodes are variables
conditional dependencies (edges)
conditional independencies (implicit)
learning
scoring metric (as MDL in ECGA)
search procedure (as merge in ECGA)
search procedure
execute primitive op. that improves the metric most
primitive op.
edge addition
edge removal
edge reversal
BOA theory
BOA solves order-k decomposable problems
in O(n
1.55) to O(n 2) evaluationsfor Hierarchical problem
hBOA (Pelikan & Goldberg, 2000, 2001)
use local structure of BN
representation for conditional prob.
|
x2 x3 P(x1=0 | x2 x3) 00 26% 01 44% 10 15% 11 15% |
x1 /\ / \ x2 x3 x2 0/\1 / \ x3 15% 0/\1 / \ 26% 44% |
Another approach
Simulaneity matrix (Aporntewan & Chongstitvatana, 2003, 2004)
<show GECCO ppt>
similar work
Dependency structure matrix (Yu & Goldberg, 2004)
Conclusion
http://www.cp.eng.chula.ac.th/~piak/
prabhas@chula.ac.th
References
Goldberg, D., Genetic algorithms, Addison-Wesley, 1989.
Whitley, D., "Genetic algorithm tutorial", www.cs.colostate.edu/~genitor/MiscPubs/tutorial.pdf
Ponsawat, J. and Chongstitvatana, P., "Solving 3-dimensional bin packing by modified genetic algorithms", National Computer Science and Engineering Conference, Thailand, 2003.
Chaisukkosol, C. and Chongstitvatana, P., "Automatic synthesis of robot programs for a biped static walker by evolutionary computation", 2nd Asian Symposium on Industrial Automation and Robotics, Bangkok, Thailand, 17-18 May 2001, pp.91-94.
Aportewan, C. and Chongstitvatana, P., "Linkage Learning by Simultaneity Matrix", Genetic and Evolutionary Computation Conference, Late Breaking paper, Chicago, 12-16 July 2003.
Aporntewan, C. and Chongstitvatana, P., "Building block identification by simulateneity matrix for hierarchical problems", Genetic and Evolutionary Computation Conference, Seattle, USA, 26-30 June 2004, Proc. part 1, pp.877-888.
Yu, Tian-Li, Goldberg, D., "Dependency structure matrix analysis: offline utility of the DSM genetic algorithm", Genetic and Evolutionary Computation Conference, Seattle, USA, 2004.
Introductory material of PMBGAs
Goldberg, D., Design of Innovation, Kluwer, 2002.
Pelikan et al. (2002). A survey to optimization by building and using probabilistic models. Computational optimization and applications, 21(1).
Larraaga & Lozano (editors) (2001). Estimation of distribution algorithms: A new tool for evolutionary computation. Kluwer.
Program code, ECGA, BOA, and BOA with decision trees/graphs http://www-illigal.ge.uiuc.edu/