AI Programming (in C)

Aim of this lecture, introduce list data structure, use of list to represent object in AI, programming with recursion to manipulate list.

List

A list is a collection of elements. An element can be an atom or another list. An atom is either "name" or "number" (other kind of atom will be introduced later). A "name" is a string. A number is an integer. A list can be printed on a screen using parentheses. This is an example of a list containing two names: "A" and "B":

( "A" "B" )

Here is many examples of list:

(1 2 3 4)
( (1 2) (3 4))
( ("A" 10) ("B" 20) ("C" 30))

The basic building block of list is a two-cell integer (called "cell"). The first cell is called "head". The second cell is called "tail". An atom has its head storing the type: name or number, and its tail storing the value. For a name, the value is an index into a string-table. For an integer, the value is the integer. A structure of a list consisted of single linked list, using two-cell (called "dot-pair" as oppossed to "atom"). The head cell stores an index to an element (can be either an atom or another list). The tail cell stores an index to the next cell. At the end of list, the tail contains a NIL value.

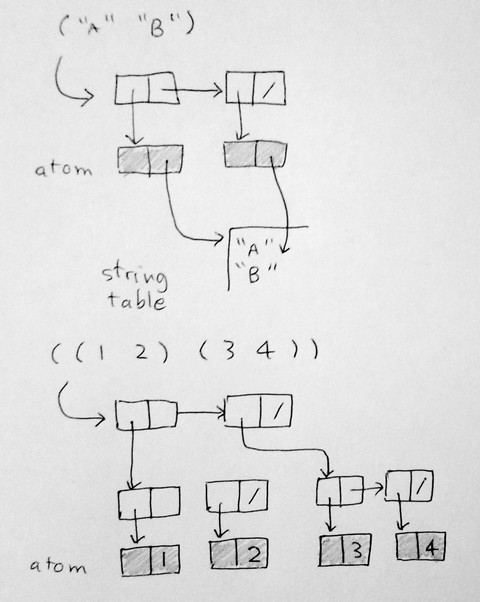
Data structure of a
list

API (application program interface)

The library (ailib.c) contains many functions to create and manipulate list.

name(string)       creates an atom "string"
number(n)          creates an atom n
list(x)                 creates a list from an element x
cons(a,b)           creates a list with its head a, its tail b
head(x)    the head of x, the first element of a list x
tail(x) the tail of x, the list x without the first element
print_list(x)        print the list x to show it on the screen
isatom(x)           return true if x is an atom
islist(x)               return true if x is a list

There is an invariant showing the relationship between head, tail and cons:

   cons(head(x), tail(x)) == x

cons(number(1), cons(number(2), cons(number(3), cons(number(4), NIL)))) == (1 2 3 4)
cons(cons(number(1), cons(number(2), NIL)),
    cons( cons(number(3), cons(number(4), NIL)), NIL))     == ((1 2 ) (3 4 ))
cons( cons(name("A"), cons(number(10),NIL)) ,
    cons( cons(name("B"), cons(number(20), NIL)),
    cons( cons(name("C"), cons(number(30),NIL)), NIL)))    == ( ("A" 10) ("B" 20) ("C" 30))

Examples

Here is an example how to create a list and show it:

#include "ailib.h"

int make_list(void){
return cons(number(1), cons(number(2), cons(number(3), cons(number(4), NIL))));
}

int main(void){
print_list( make_list() );
}

Set up your C compiler IDE environment, including "ailib.c" and "ailib.h" at the same directory as the application program.
Now, we will make a simple program to count the number of elements of a simple list.

int len(int ls){
if(ls == NIL) return 0;
else return 1 + len(tail(ls));
}

int test_len(void){
int a;
a = make_list();
printf("%d\n", len(a));
}

The "len" function works like this: using a case analysis, if the list is empty (NIL) the number of element is 0, otherwise it is one pluses the length of the rest of the list (tail(ls)).

Now we extend the "len" to cope with a complex list (its element can be another list).

int len2(int ls){
if(ls == NIL) return 0;
if(isatom(ls)) return 1;
else return len2(head(ls)) + len2(tail(ls));
}

int make_complex_list(void){
int a, b;
a = cons(number(1),cons(number(2),NIL));
b = cons(number(3),cons(number(4),NIL));
return cons(a, cons(b, NIL));
}

void test_len_complex(void){
int a;
a = make_complex_list();
printf("%d\n", len(a));
printf("%d\n", len2(a));
}

If we apply "len" to a complex list, it will count the element, if an element is a list, it counts as one. "len" does not get "into" the element when it is a list. "len2" checks if an element is a list, it is recursively walking into that list and count its element.

The "len" function shows us how to traverse the list structure recursively. Next, we learn how to "create" a duplicate of a list (using "cons"). It is quite similar to "len". Start with a simple list. We introduce a new function:

clone_atom(x) creates a duplicate of an atom x

int copy_list(int ls){
if(ls == NIL) return NIL;
else return cons(clone_atom(head(ls)), copy_list(tail(ls)));
}

void test_copy(void){
int a, b;
a = make_list();
b = copy_list(a);
print_list(a);
}

We can extend "copy_list" to cope with a complex list, not much different from "len2".

int copy_list_complex(void){
if(ls == NIL) return NIL;
if(isatom(ls)) return clone_atom(ls);
else return cons( copy_list_complex, copy_list_complex(tail(ls)));
}

void test_copy_complex(void){
int a, b;
a = make_list_complex();
b = copy_list2(a);
print_list(b);
}

If the list is empty "copy_list_complex" terminates by returning a NIL. If input is an atom, return a duplicate of that atom. Otherwise the list is complex, walk into the first element and make a duplicate (recursively), and do the rest of the list, then "cons" them together. The "copy_list_complex" can copy a list with an arbitrary length and shape!

Some excercises

1)   Write a program to increment one of all elements of a simple list of integers. (1 2 3 4) => (2 3 4 5)
2) Write a program to reverse a simple list. (1 2 3 4) => (4 3 2 1)
3)    Write a program to divide a simple list into a list with two elements, each is a list containing half of element of the original. (assuming the length of the input list is a even number)
4)    Write a search function of an "associative list". An associative list contains a list of records, a record is a pair of: the first element is a "key" which is a a name, the second element is the value, an integer. Given a key, find the value associate with that key. Here is an example:

a = cons(name("mango"), cons(number(3), NIL));
b = cons(name("orange"), cons(number(5), NIL));
table = cons(a, cons(b, NIL));

a table is ( ( "mango" 3 ) ("orange" 5) )

search(table, name("orange")) => 5
search(table, name("ice cream")) => NIL

This is different from an ordinary array which index must be integer.

Enjoy!

last update 17 Oct 2011