Processor Design

S1 simple cpu

To illustrate how a processor can be designed, we will desribe the design of a simple hypothetical CPU called S1.  S1 contains all the important elements of a real processor.  It is aimed to be as simple as possible so that students can understand it easily.  The architectural description of S1 : its organization (structure), its instruction set (ISA) and its behaviour (micro steps), is small enough to fit into a few pages. A simulator of S1 at instruction level is also provided.  Studying how the simulator work will enable students to modify and design their own processor.

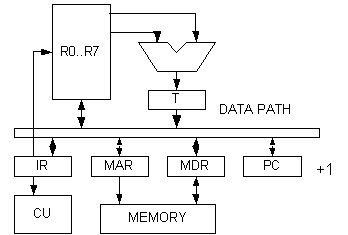
Instruction set design

Instruction format
1) op:3, r0:3, ads:10
    15..13 12..10 9..0
    op     r0     ads
2) op:3, xop:4, r1:3, r2:3
    15..13 12..9 8..6 5..3 2..0
    7      xop   0    r1   r2

instruction                  op
load M, r       0     M -> r
store r, M      1     r -> M
jump c, ads     2
call 0, ads     3     push(PC), goto ads
xop             7

mov r1,r2       0     r1 -> r2
load (r1),r2    1     (r1) -> r2  load indirect
store r1,(r2)   2     r1 -> (r2)  store indirect
add r1,r2       3     r1 + r2 -> r1
cmp r1,r2       4     compare, affect Z,S
inc r1          5
ret             6     pop(PC)

r 0..7
c 0..6  conditional : 0 always, 1 Z, 2 NZ, 3 LT, 4 LE, 5 GE, 6 GT
M/ads 0..1023  address space

S1 microarchitecture

We study the operation of a hypothetical CPU in details, at the level of events happening every clock cycle when the CPU executes an instruction.  Our description is in the form of Register Transfer Language (RTL) which represent the event of data movement inside a processor.  Naturally, the description at this level of abstraction involves time.  Each line of event happens in one unit of time (clock). We call this description "micro step".

Notation
// comment
dest = source   // data move from source to destination
e1 ; e2         // event e1 and e2 occur on the same time
M[a]            // memory at the address a
IR:a            // bit field specified by a of IR
<name>          // macro name
op()            // ALU function

// main loop
repeat
  <ifetch>
  <decode>
  <execute>

<ifetch>
  MAR = PC
  MDR = M[MAR]    // MREAD
  IR = MDR ; PC = PC + 1

<load>
  MAR = IR:ADS
  MDR = M[MAR]
  R[IR:R0] = MDR

<store>
  MAR = IR:ADS
  MDR = R[IR:R0]
  M[MAR] = MDR    // MWRITE

<loadr>
  MAR = R[IR:R1]
  MDR = M[MAR]
  R[IR:R2] = MDR

<storer>
  MDR = R[IR:R2]
  MAR = R[IR:R1]
  M[MAR] = MDR

<move>
  T = R[IR:R1]
  R[IR:R2] = T

<add>
  T = add(R[IR:R1], R[IR:R2])
  R[IR:R1] = T

<compare>
  CC = cmp(R[IR:R1], R[IR:R2])    // condition code set

<increment>
  T = inc(R[IR:R1])
  R[IR:R1] = T

<jump>
  if testCC(IR:R0)
  then PC = IR:ADS

<call>
  T = add1(R[7])
  R[7] = T
  MAR = R[7]  // sp+1 then put stack
  MDR = PC
  M[MAR] = MDR
  PC = IR:ADS

<return>
  MAR = R[7]
  MDR = M[MAR]  // get stack then sp-1
  PC = MDR
  T = sub1(R[7])
  R[7] = T

// instruction fetch can be faster
<ifetch2>
  MAR = PC
  IR = MDR = M[MAR]; PC = PC + 1

TIMING of S1   unit clock (count ifetch as 3 clocks)
load            6
store           6
jmp             5
call            9
mov r r         5
load (r) r      6
store r (r)     6
add             5
cmp             4
inc             5
ret             8

Call and return take the longest time in the instruction set.  Calling a subroutine can be made faster by inventing a new instruction that does not  keep the return address in the stack (and hence the memory) but keeping it in the register instead.  Jump and link (JAL) just saves the return address in a specified register and jump to the subroutine.  Jump Register (JR) then does the reverse.  It does the job of the "return" instruction. The register that stored return address must be saved to the memory (i.e. manage by the programmer) if the call to subroutine can be nested.  This will reduce the clock to 5 for "jal" and 4 for "jr".  This shows that using registers can be much faster than using the memory.

jal r, ads    store PC in r and jump to ads
jr r          jump back to (r)

<jal>
  R[IR:R1] = PC
  PC = IR:ADS

<jr>
  PC = R[IR:R1]

Example of an assembly program for S1.  Find sum of an array : sum a[0] .. a[N]
sum = 0
i = 0
while ( i < N )
  sum = sum + a[i]
  i = i + 1

        .ORG 0            // address  code
        load ZERO r0     0  0 0 20
        store r0 SUM     1  1 0 21
        store r0 I       2  1 0 22
        load N r1        3  0 1 23
        load I r3        4  0 3 22
loop    cmp r3 r1        5  7 4 3
        jmp GE endwhi    6  2 5 16
        load BASE r2     7  0 2 24
        add r2 r3        8  7 3 2 3
        load (r2) r4     9  7 2 2 4
        load SUM r5      10 0 5 21
        add r5 r4        11 7 3 5 4
        store r5 SUM     12 1 5 21
        inc r3           13 7 5 3 0
        store r3 I       14 1 3 22
        jump loop        15 2 0 5
endwhi  load SUM r0      16 0 0 21
        call print       17 3 0 1001
        call stop        18 3 0 1000

        .ORG 20  // data
ZERO    0                20 0
SUM     0                21 0
I       0                22 0
N       100              23 100
BASE    25               24 25
a[..]   a[0]             25 a[0]
        a[1]             26 a[1]
        ...              ...

S1 runs 1110 instruction with 5963 clocks, CPI = 5.37
 

How to run the S1 simulator

     The input file is an object file with the name "in.obj".  When run s1  the simulator will start and load "in.obj" and execute starting from PC=0 until stop with the instruction call 1000

  An object file has the following format
a  ads         set PC to ads
i  op r ads      instruction op
i  7 xop r1 r2   instruction xop
w  data         set that address to value "data"
t              set trace mode on
d  start nbyte   dump memory n byte
e              end of object file

Be careful, the input routine is not robust.  A malformed input line can caused unpredictable result.  The input loop is limited to 200 words (to prevent infinite loop).