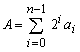
The arithmetic logic unit (ALU) is the part of the processor that performs calculation both the arithmetic and the logic operations. It composed of functional units and registers including some status bit for storing the result of operations such as zero and overflow. The functional units included adder, multiplier and shifter. As an ALU is realised using logic gates, it relies on the computer arithmetic algorithms to perform calculation by repetition such as using multiple add-shifts to do multiplication. This enables complex calculations such as floating point operations possible on an economical hardware.

A is expressed in a decimal number. The base is 10. This representation has 10 symbols 0, 1, 2, … 9 which constitutes digits.

A number is represented as sum of weights that are a power of 2. The base is 2 and there are two symbols 0, 1 called binary digits or bits.

A number can be represented by n-bit in many ways. For an integer, there are unsigned, sign-magnitude and two's complement representation.

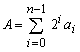
An unsigned integer ranges over non negative numbers. For n-bit integer its range is 0…2^{n -} 1.

The left most bit is sign, the right most n- 1 bit is magnitude. It has several drawbacks. First addition and subtraction require special treatment of sign and relative magnitudes. Second, the number zero has two representations +0, - 0.

We have seen how to represent an unsigned integer but how a negative number can be represent without using sign-magnitude? Suppose we have 3-bit binary a₂a₁a₀ which can represent 2³ - 8 positive numbers for 000 to 111 (0 to 7). The fourth bit can be introduced to associate with the negative weight - 2³. The 4-bit number can represent 1000₂ ( - 8₁₀ ) to 0111₂ ( +7₁₀ ). The decimal value is

The number is negative is A₃ = 1. The properties of this representation are

1. Bit A₃ gives the sign of the equivalent decimal number, A₃ =1 negative, A₃ = 0 positive.
2. There is one zero and it is positive.
3. A positive decimal number is changed to a negative number of the same absolute value by inverting each bit followed by adding a 1.

Figure 3.1 4-bit two complement numbers

Example Convert 110₂ (+6₁₀) to a negative number - 6₁₀.

0010 inverse to 1001, 1001 plus 1 is 1010₂ = - 6₁₀

This number is called two's complement of the original number.

The following expression defines the two's complement representation for both positive and negative numbers. if A is positive, the sign bit (a _n-1) is zero. The range of positive number is 0 … 2 ^n-2 . The range of negative number is - 1 … - 2 ^n-1 .

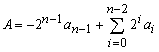
Using two's complement representation, subtraction is performed by adding the two's complement. For example, 5 - 3 = 2, (+5) + (- 3) = 2, (0101) + (1101) = 10010. The left most bit (carry bit) is overflowed. We ignore the overflow and the result is 0010 = 2. On any addition, the result may be larger than can be held in the word size being used. This condition is called overflow. When overflow occurs, the ALU signals the condition codes. The overflow rule is: If two numbers are added, and they are both positive or both negative, then overflow occurs if and only if the result has the opposite sign.

Subtraction is achieved using addition. We can demonstrate by the following example. If B = - A, then A + B = A + (- A) = 0. For n-bit integer, B is a bitwise complement of A plus 1, that is - A. Let a_n' be a complement of a_n .

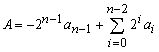
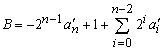
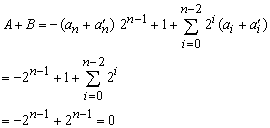
Multiplication is a complex operation. Multiplication firstly generates partial products, one for each digit in the multiplier, then summed them to produce the final product. Each successive partial product is shifted one position to the left relative to the preceding partial product. The multiplication of a binary number 2ⁿ is accomplished by shifting that number to the left by n bits. The multiplication of two n-bit integers results in a product of up to 2n bits in length.

Figure 3.2 Multiplication of unsigned integers

One of the well-known algorithms for two's complement multiplication is Booth's algorithm [BOO51]. Let Q, M, A be three n-bit registers, Q stores multiplier, M multiplicand, the result appears in AQ. A concatenates to Q and when shifting right, the least significant bit of A will go to the most significant bit of Q. There is one bit placed to the right of the least significant bit of Q (Q0), designated Q-. Booth's algorithm is as follows:

Note the efficiency of the algorithm. Blocks of 1s or 0s are skipped over, with an average of one addition or subtraction per block.

Observe that the number to partial product sum can be reduce. Consider a positive multiplier where one contiguous 1s surrounded by 0s. The number of shift-and-add can be reduced by observing that

The product can be generated by one addition and one subtraction of the multiplicand. Booth's algorithm performs subtraction when first 1 of block is encountered (1-0) and addition when the end of block is encountered (0-1). This scheme extends to any number of blocks of 1s in a multiplier and negative number.

The division is based on the long division. It involves repetitive shifting and addition or subtraction. Dividend is examined bit by bit from left to right until it is greater than or equal to the divisor, 0s are placed in the quotient, when it is divisible, 1 is placed in the quotient and the divisor is subtract from the partial dividend. Additional bits from the dividend are appended to the partial remainder until the result is greater than or equal to the divisor then the cycle repeat.

0 0 0 0 1 1 0 1 Quotient

Divisor 1 0 1 1 / 1 0 0 1 0 0 1 1 Dividend

1 0 1 1

Partial remainders 0 0 1 1 1 0

1 0 1 1

0 0 1 1 1 1

1 0 1 1

1 0 0 Remainder

Figure 3.4 Division of unsigned binary integers

The algorithm is as follows:

end {quotient in Q, remainder in A}

This scheme, with some difficulty, can be extended to negative numbers. The divisor must be expressed as 2n-bit two's complement number.

if (divisor and dividend are not same sign) then two's complement Q

end {quotient is in Q, remainder is in A }

Very large and very small numbers can be represent using scientific notation which separately store significand and exponent, such as 2.14 * 10¹² . This allow a range of very large and very small numbers to be represented using only a few digits. In binary numbers, a number is represent in the form:

This number can be stored in a binary word using three fields: Sign bit, Significand and Exponent. The base is implicit. The exponent can be stored with bias, i.e. a bias is subtracted from the field to get the true value. An example of 32-bit floating-point format is 1 bit sign, 8 bits biased exponent and 23 bits significand. The bias is 128.

0.11010001 ´ 2 ¹⁰¹⁰⁰ = 0 10010100 10100010000000000000000

0.11010001 ´ 2 - ¹⁰¹⁰⁰ = 0 01101100 10100010000000000000000

Figure 3.6 an example of 32-bit floating-point format

Therefore the left most bit of significand is always 1 and is "implicit" (no need to store this bit).

With the above representation the following ranges of numbers are possible:

Negative numbers between - (1 - 2 - ²⁴) ´ 2 ¹²⁷ and - 0.5 ´ 2 - ¹²⁸

Positive numbers between 0.5 ´ 2 - ¹²⁸ to (1 - 2 - ²⁴) ´ 2 ¹²⁷

Five regions on the number line are not included in these ranges:

• Negative numbers less than - (1 - 2 - ²⁴) ´ 2 ¹²⁷ , called negative overflow
• Negative numbers greater than - 0.5 ´ 2 - ¹²⁸ , called negative underflow
• Zero
• Positive numbers less than 0.5 ´ 2 - ¹²⁸ , called positive underflow
• Positive numbers greater than (1 - 2 - ²⁴) ´ 2 ¹²⁷ , called positive overflow

Remember that the maximum number of different values that can be represented with 32 bits is still 2 ³². The numbers represented in floating-point notation are not spaced evenly along the number line. The possible values get closer together near the origin and farther apart as you move away. This is one of the trade-off of floating-point: Many calculations produce results that are not exact and have to be rounded to the nearest value that the notation can represent.

The most important floating-point representation is defined in IEEE Standard 754 [IEE85]. The IEEE standard defines both a 32-bit single and a 64-bit double format. The single format has a sign bit, 8-bit biased exponent, 23-bit significand. The exponent bias is 127. The double format has a sign bit, 11-bit biased exponent, 52-bit significand. The exponent bias is 1023. The implied base is 2. The standard defines two extended formats, single and double, whose exact format is implementation-dependent. The extended formats are to be used for intermediate calculations.

There are some bit patterns that are used to represent special numbers such as zero, plus/minus infinity, NaN (not a number) and denormalized number etc.

Figure 3.7 special numbers of IEEE 754 (double precision)

For addition and subtraction, it is necessary for both operands to have the same exponent. This may require shifting the radix point to achieve the alignment. The multiplication and division are more straightforward. When the significand is underflow the rounding operation is required. Likewise when it is overflow the realignment (normalized) is required.

There are four basic phases of the algorithm for addition and subtraction:

1. Check for zeros
2. Align the significands
3. Add or subtract the significands
4. Normalized the result

The addition-subtraction algorithm is as follows:

The multiplication and division are simpler than addition and subtraction. The multiplication algorithm is as follows:

For the floating-point operations the significands are loaded into the registers. The length of the register is almost always greater than the length of significand plus an implied bit. The register contains an additional bit, called guard bits, the are used to pad out the right end of the significand with 0s. The purpose is to prevent the lost of least significant bit when one operand must be shifted right during floating-point operation. As seen from the following example: a subtraction without and with guard bits.

The rounding policy affects the precision of the result. IEEE standard lists four approaches:

• Round to nearest - to the nearest representable number
• Round toward positive infinity
• Round toward negative infinity
• Round toward 0 (truncated)

Round to the nearest is the default rounding mode in the standard. The rounding to plus and minus infinity is useful in implementation of interval arithmetic. In the interval arithmetic an upper bound and lower bound on the correct answer are kept. If the range between the upper and lower bounds is sufficiently narrow, it indicates that a sufficiently accurate result is obtained.

Denormalized numbers are included in IEEE 754 to handle E underflow, the result is denormalized by right-shifting S and increment E until E is within representable range. This method is also referred to as "gradual underflow" [COO81].