Genetic
programming is a branch of genetic algorithms.
The main difference between genetic programming and genetic algorithms
is
the representation of the solution. Genetic programming creates
computer
programs in the lisp or scheme computer languages as the solution.
Genetic
algorithms create a string of numbers that represent the solution.
Genetic
programming, uses four steps to solve problems:
1) Generate an initial population of random compositions of the functions and terminals of the problem
(computer programs).
2) Execute each program in the population and assign it a fitness
value according to how well it solves the problem.
3) Create a new population of computer programs.
i) Copy the best existing programs
ii) Create new computer programs by mutation.
iii) Create new computer programs by crossover(sexual
reproduction).
4) The best computer program that appeared in any generation, the
best-so-far
solution, is designated as the result of genetic programming [Koza
1992].
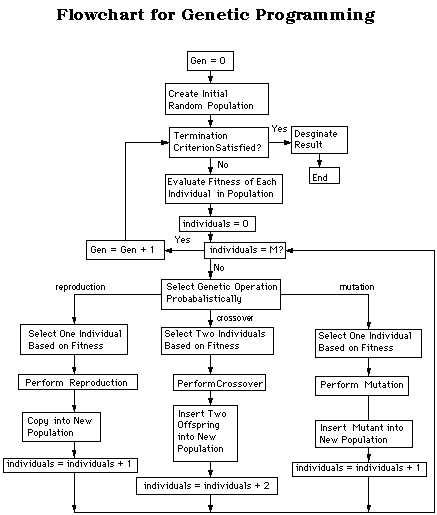
Figure 1: genetic programming Flowchart.
Fitness Function
The most difficult and most important concept of
genetic programming is the fitness function. The fitness function
determines how well a program is able to solve the problem. It varies
greatly from one type of program to the next. For example, if one were
to create a genetic program to set the time of a clock, the fitness
function would simply be the amount of time that the clock is wrong.
Unfortunately, few problems have such an easy fitness function; most
cases require a slight modification of the problem in order to find the
fitness.
Gun Firing Program
A more complicated example consists of training a
genetic program to fire a gun to hit a moving target. The fitness
function is the distance that the bullet is off from the target. The
program has to learn to take into account a number of variables, such
as wind velocity, type of gun used, distance to the target, height of
the target, velocity and acceleration of the target. This problem
represents the type of problem for which genetic programs are best. It
is a simple fitness function with a large number of variables.
Water Sprinkler System
Consider a program to control the flow of water through
a system of water sprinklers. The fitness function is the correct
amount of water evenly distributed over the surface. Unfortunately,
there is no one variable encompassing this measurement. Thus, the
problem must be modified to find a numerical fitness. One possible
solution is placing water-collecting measuring devices at certain
intervals on the surface. The fitness could then be the standard
deviation in water level from all the measuring devices. Another
possible fitness measure could be the difference between the lowest
measured water level and the ideal amount of water; however, this
number would not account in any way the water marks at other measuring
devices, which may not be at the ideal mark.
Maze Solving Program
If one were to create a program to find the solution to
a maze, first, the program would have to be trained with several known
mazes. The ideal solution from the start to finish of the maze would be
described by a path of dots. The fitness in this case would be the
number of dots the program is able to find. In order to prevent the
program from wandering around the maze too long, a time limit is
implemented along with the fitness function.
Functions and Terminals
The terminal and function sets are also important
components of genetic programming. The terminal and function sets are
the alphabet of the programs to be made. The terminal set consists of
the variables and constants of the programs. In the maze example, the
terminal set would contain three commands: forward, right and left. The
function set consists of the functions of the program. In the maze
example the function set would contain: If "dot" then do x else do y.
In the gun firing program is the terminal set would be composed of the
different variables of the problem. Some of these variables could be
the velocities and accelerations of the gun, the bullet and target. The
functions are several mathematical functions, such as addition,
subtraction, division, multiplication and other more complex functions.
Crossover Operation
Two primary operations exist for modifying structures
in genetic programming. The most important one is the crossover
operation. In the crossover operation, two solutions are sexually
combined to form two new solutions or offspring. The parents are chosen
from the population by a function of the fitness of the solutions.
Three methods exist for selecting the solutions for the crossover
operation.
The first method uses probability based on the fitness of the solution.
If  is the fitness of the solution
Si and is the fitness of the solution
Si and
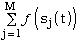
- is the total sum
of all the members of the population, then the probability that the
solution Si will be copied to the next generation is [Koza 1992]:
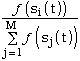
Another method for selecting the solution to be copied is tournament
selection. Typically the genetic program chooses two solutions random.
The solution with the higher fitness will win. This method simulates
biological mating patterns in which, two members of the same sex
compete to mate with a third one of a different sex. Finally, the third
method is done by rank. In rank selection, selection is based on the
rank, (not the numerical value) of the fitness values of the solutions
of the population [Koza 1992].
The creation of the offsprings from the crossover operation is
accomplish by deleting the crossover fragment of the first parent and
then inserting the crossover fragment of the second parent. The second
offspring is produced in a symmetric manner. For example consider the
two S-expressions in Figure 2, written in a modified scheme programming
language and represented in a tree.
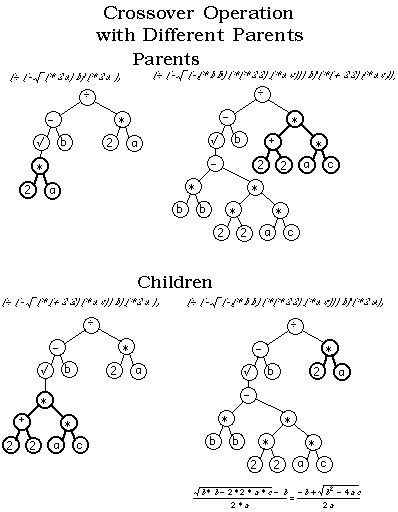
Figure
2:
Crossover operation for genetic programming.
The bold selections on both parents are swapped to create the offspring
or children. (The child on the right is the parse tree representation
for
the quadratic equation.)
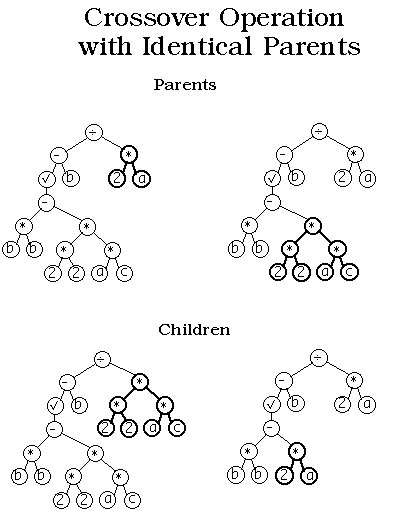
Figure
3: This figure illustrates one of the
main advantages of genetic programming
over genetic algorithms. In genetic programming
identical parents can yield different offspring,
while in genetic algorithms identical parents
would yield identical offspring. The bold
selections indicate the subtrees to be
swapped.
An important improvement that genetic programming displays over genetic
algorithms is its ability to create two new solutions from the same
solution. In the Figure 3 the same parent is used twice to create two
new children.
Mutation
Mutation is another important feature of genetic programming. Two types
of mutations are possible. In the first kind a function can only
replace a function or a terminal can only replace a terminal. In the
second kind an entire subtree can replace another subtree. Figure 4
explains the concept of mutation:
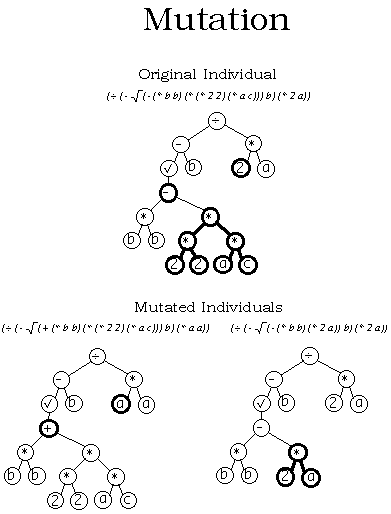
Figure
4:
Two different types of mutations. The top parse
tree is the original agent. The bottom left parse tree illustrates a
mutation
of a single terminal (2) for another single terminal (a). It also
illustrates
a mutation of a single function (-) for another single function (+).
The
parse tree on the bottom right illustrates a the replacement of a
subtree
by another subtree.
Summary
Genetic programming is much more powerful than genetic algorithms. The
output of the genetic algorithm is a quantity, while the output of the
genetic programming is a another computer program. In essence, this is
the beginning of computer programs that program themselves.
Genetic programming works best for several types of problems. The first
type is where there is no ideal solution, (for example, a program that
drives a car). There is no one solution to driving a car. Some
solutions drive safely at the expense of time, while others drive fast
at a high safety risk. Therefore, driving a car consists of making
compromises of speed versus safety, as well as many other variables. In
this case genetic programming will find a solution that attempts to
compromise and be the most efficient solution from a large list of
variables.
Furthermore, genetic programming is useful in finding solutions where
the variables are constantly changing. In the previous car example, the
program will find one solution for a smooth concrete highway, while it
will find a totally different solution for a rough unpaved road.

REFERENCES
Koza, John R. 1992. Genetic Programming: On the
Programming of Computers by Means of Natural Selection. Cambridge,
MA: The MIT Press.
Cramer, Nichael Lynn: "A Representation for the Adaptive Generation of
Simple Sequential Programs", Proceedings, International Conference on
Genetic Algorithms and their Applications, July 1985 [CMU], pp183-187.
|
![]()