Writing a parser from a parsing table

A parsing table is like a state-transition table of a Finite State Machine. The rules (non-terminal symbols) is the current state.  The input is the input for FSM. The value in the table is the next state. 

So, to "run" the parser, the main loop is similar to simulate FSM step-by-step. The main loop is:

main()
  initialise state
  while( not error and not end-state )
    s = lookup parsing-table (state,input)
    switch( s )
      case 1 : do..
      case ...

Each "action routine" is the execution of the rule.  This is the simulation of a state-machine (parser) on a stack.  The stack contains the remaining work of the parser.  The stack begin with "end-of-input" and the first rule is the starting symbol.

For example let us write a parser for this simple grammar.

exp -> term exp'
exp' -> addop term exp' | empty
addop -> + | -
term -> factor term'
term' -> mulop factor term' | empty
mulop -> *
factor -> ( exp ) | num

The First and Follow set and the parsing table of this grammar is shown here.

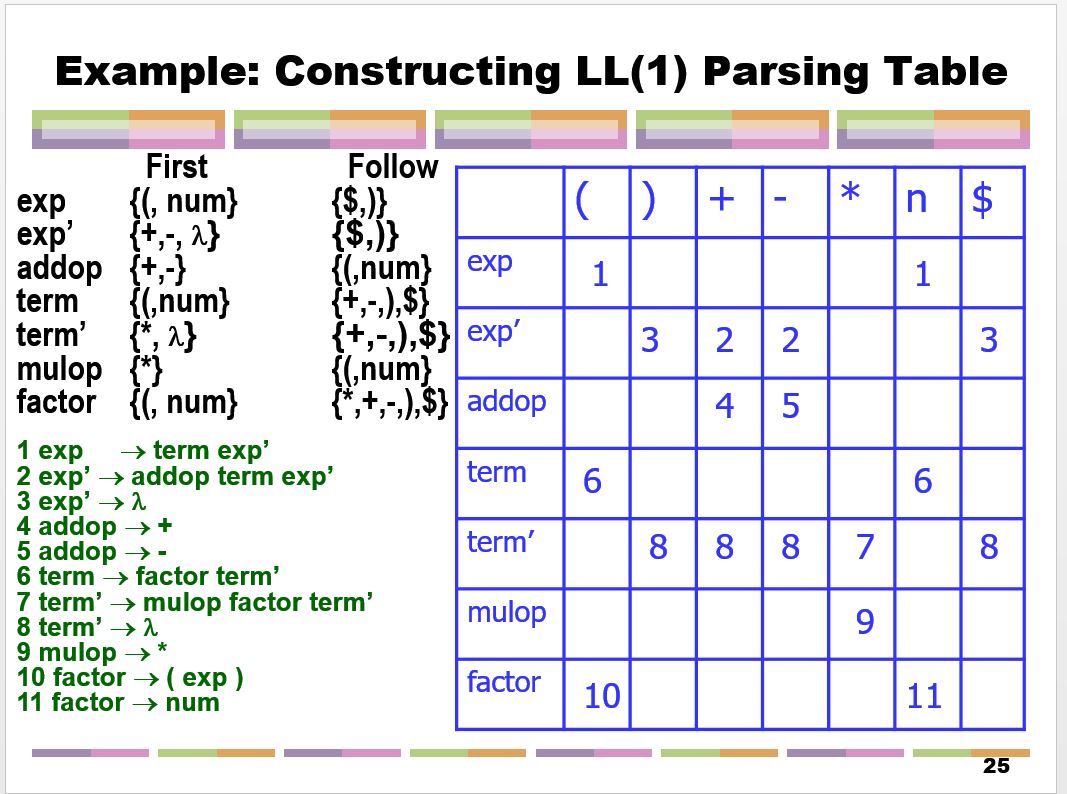
< figure slide 25 >

We implement each rule as a function. The action routines in the main loop is just a call to these functions.

main()
  while( ... )
    s = lookup(state,input)
    switch( s )
      case 1: exp()
      case 2: exp2_1()
      case 3: exp2_2()
      .....
      case 11: match('num')

Each rule implements actions on the stack following the grammar.

exp()    // rule 1
  pop
  push #exp2
  push #term

exp2_1()   // rule 2
  pop
  push #exp2
  push #term
  push #addop

...

factor_1()  // rule 10
  pop
  push ')'
  push #exp
  push '('

factor_2()  // rule 11
  pop
  push 'num'

Please notice that the "reverse" order of the push action on the stack. You must push the right most item first.

What to do when encounter a terminal symbol on the stack?  We just check that it "match" with the current input token.  Then, pop the stack, advance the input (getToken).  If the error occurs (reach state = 0) the parser just stop. When the parser stops, if the stack match "end-of-input" then it is successful, otherwise it fails.

Details of the implementation

The stack holds the ID of the rules which are just a number signifies the rule. The "switch-case" in the main loop binds these numbers to the correct function calls. 

getToken() is a function of the scanner.  It returns a value which is the value of the token, for example, ',' token has value 66.  The parsing table is just a two-dimension array of rule IDs (state). The value 0 denotes an error.  The actual code (I wrote it in C) can be download from the website of the class.

Example session

After getting an executable parser (parser.exe).  We use a console to run the parser with an input.

Let the input file be:

n + n * n ;

We denote the "end-of-input" by ';'

c:> parser test.txt

Here is what appear on the screen:

n <<exp eol >>
[1] <<term exp2 eol >>
[6] <<factor term2 exp2 eol >>
[11] <<n term2 exp2 eol >>
+ <<term2 exp2 eol >>
[8] <<exp2 eol >>
[2] <<addop term exp2 eol >>
[4] <<+ term exp2 eol >>
n <<term exp2 eol >>
[6] <<factor term2 exp2 eol >>
[11] <<n term2 exp2 eol >>
* <<term2 exp2 eol >>
[7] <<mulop factor term2 exp2 eol >>
[9] <<* factor term2 exp2 eol >>
n <<factor term2 exp2 eol >>
[11] <<n term2 exp2 eol >>
eol <<term2 exp2 eol >>
[8] <<exp2 eol >>
[3]

Each line shows a step of parsing (or a step of derivation).  The stack values is shown in <<...>> with the top of stack on the left hand side, for example <<exp eol>> -- exp is the top of the stack and eol is "end-of-input".

The first line reads:
n <<exp eol >>

bottom of the stack is "end-of-input"
the first rule to take action is "exp" (the start symbol of the grammar).
the current input is "n"

looking up the parsing table the next state is "rule 1", the right hand side of the rule is placed on the stack.

Here is the second line:
[1] <<term exp2 eol >>

Rule 1 is used, it places "term exp2" on the stack

The next state is Rule 6, looking up the parsing table with the top of stack "exp" and the input "n" results in Rule 6. The stack is adjusted, placing RHS of "term" ("factor term2") on the stack.

[6] <<factor term2 exp2 eol >>

and the next state is Rule 11.

[11] <<n term2 exp2 eol >>

now the top of stack is a terminal symbol "n"
and the current input is "n".
the action is matching the two. poping the terminal symbol from the stack. Advancing the input to the next token. Here is the next state.

+ <<term2 exp2 eol >>

and so on.  Until it reaches the near final state.

eol <<term2 exp2 eol >>
[8] <<exp2 eol >>
[3]

now the input is "end-of-input". Rule 8 just pops "term2" out of the stack. Then Rule 3 pops "exp2". The final state is reached as the top of the stack matches the input. The parser is successfully parsed the input.
 
Please play with the source code, build the program and test it out yourself.

PS the updated package  LL1-parser-2.zip  works on both Windows 10 and MacOS (I use xcode to compile on Mac). The executable file for Mac is used this way, on Mac opens a terminal:  

$ ./xparser test.txt

Enjoy

last update 14 Apr 2020