Approximation Algorithm
Euclidean Traveling Salesperson Problem
ปัญหาการเดินทางของพนักงานขายในตัวอย่างนี้ เราสนใจเฉพาะกรณีเมื่อความยาวของเส้นเชื่อมระหว่างเมืองสองเมืองใดคือระยะขจัดของตำแหน่งของเมืองบนระนาบแบบยุคลิด (Euclidean plane) ซึ่งหมายความว่าความยาวของเส้นเชื่อมต่างๆ ที่เชื่อมเมืองสามเมืองใดๆ ต้องเป็นไปตามอสมการอิงรูปสามเหลี่ยม (triangle inequality)นั่นคือผลรวมของความยาวด้านสองด้านใดๆ ต้องไม่น้อยกว่าด้านที่สาม
ด้วยเงื่อนไขที่เพิ่มเข้าไปเช่นนี้ก็ยังคงทำให้ปัญหานี้เป็น NPhard แต่ทำให้เราสามารถหาอัลกอริทึมเชิงประมาณแบบ 2 (2-approx algo) ได้ง่ายมากๆ ดังนี้
public class TSP_MSTApprox {
public static int[] getTour(double[][] g) { // g is a graph boolean[][] mst = findMST(g); int[] tour = new int[g.length]; preorder(mst, 0, tour); // traversal starts at vertex 0 return tour; } ... }
เริ่มด้วยการหาต้นไม้แบบทอดข้ามเล็กสุดของกราฟ จากนั้นจะได้ว่าการเดินทางของพนักงานขายก็คือลำดับของการแวะผ่านจุดในต้นไม้นี้แบบก่อนลำดับ รูปที่ 1312ก แสดงจุด 13 จุด ซึ่งมีเส้นเชื่อมต่อถึงกันหมด (ไม่ได้แสดงเส้นเชื่อมในรูป) หลังจากนั้นหาต้นไม้แบบทอดข้ามเล็กสุดจะได้ดังรูปที่ 1312 ข ถ้าให้จุดหมายเลข 1 เป็นรากแล้วแวะผ่านแบบก่อนลำดับจะได้ลำดับจุดที่แวะผ่านคือ 1, 2, 3, ..., 12, 13 จะได้การเดินทางของพนักงานขายเชิงประมาณแสดงดังรูปที่ 1312ค
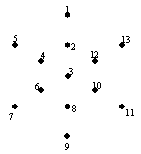
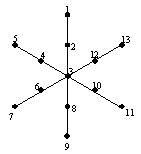
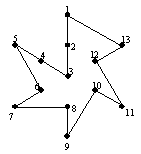
(ก) (ข) (ค)
รูปที่ 1312 การเดินทางของพนักงานขายเชิงประมาณ
เราจะแสดงให้เห็นจริงว่าการเดินทางที่ได้จาก getTour( ) นั้นยาวไม่เกินสองเท่าของการเดินทางที่สั้นสุด ก่อนอื่นของกำหนดสัญลักษณ์ที่จะใช้อ้างอิงดังต่อไปนี้
· TMST คือต้นไม้แบบทอดข้ามเล็กสุดต้นหนึ่งของกราฟ
· TTSP คือการเดินทางที่หาได้จาก getTour( )
· LMST เป็นผลรวมของความยาวของเส้นเชื่อมทุกเส้นใน TMST
· LTSP เป็นระยะทางของการเดินทาง TTSP
· LOPT คือระยะทางรวมของการเดินทางของพนักงานขายที่สั้นสุด
เนื่องจากการเดินทางของพนักงานขายเป็นวงจรในกราฟ ถ้าเราตัดเส้นเชื่อมที่ยาวที่สุดในวงจรนี้ออก ก็ย่อมเป็นต้นไม้ (เป็นต้นไม้ที่เป็นเส้นยาวต่อกันไป) และต้นไม้นี้ย่อมต้องเป็นต้นไม้แบบทอดข้ามด้วย (เพราะเป็นทางเดินที่ผ่านทุกจุด) แต่ไม่จำเป็นต้องเป็นต้นไม้แบบทอดข้ามเล็กสุด ดังนั้น LOPT ³ LMST ถ้าเราเริ่มที่รากของ TMST แล้ววิ่งไปตามเส้นเชื่อมในลักษณะตามแนวลึก โดยเมื่อพบทางตันก็วิ่งย้อนกลับอีกด้านของเส้นเชื่อมขึ้นมา ผ่านทั้งสองด้านของเส้นเชื่อมในลักษณะนี้ไปเรื่อยๆ จนมาจบที่ราก ตัวอย่างเช่นเส้นประใน รูปที่ 1313ก แสดงวิถีการเลื้อยตามเส้นเชื่อมของต้นไม้ในรูป จะได้ว่าวิถีการเลื้อยบน TMST นี้ย่อมมีความยาวรวมเป็นสองเท่าของความยาวรวมของเส้นเชื่อมของต้นไม้ซึ่งเท่ากับ 2LMST
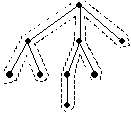
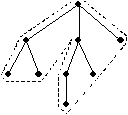
(ก) (ข)
รูปที่ 1313 วิถีการเดินตามเส้นเชื่อม (ก) และการเดินลัด (ข)
แต่เนื่องจากการเดินทางของพนักงานจะต้องผ่านเมืองละครั้งแบบไม่ซ้ำ ดังนั้นแทนที่จะเดินตามเส้นเชื่อมในลักษณะข้างต้น คือย้อนกลับเมืองเดิมเพื่อไปเมืองใหม่ ก็สามารถเดินลัดตรงไปเมืองใหม่ได้เลย เส้นประในรูปที่ 1313ข แสดงเส้นทางลัดของการเดินทางในรูปที่ 1313ก และเป็นการเดินทางซึ่งไม่ผ่านเมืองซ้ำกัน โดยเรามั่นใจได้แน่ๆ ว่าเส้นทางลัดนี้ต้องไม่ยาวกว่าแบบเดินย้อน ทั้งนี้เพราะเงื่อนไขของอสมการของสามเหลี่ยมนั่นเอง การเดินลัดแบบนี้จะมีลำดับของเมืองที่ผ่านตามลำดับการแวะผ่านแบบก่อนลำดับ
สรุปได้ว่า LTSP £ 2LMST และ LMST £ LOPT ดังนั้น LTSP £ 2LOPT
สมชาย
ประสิทธิ์จูตระกูล
2110427 :
การวิเคราะห์และออกแบบอัลกอริทึม