[การวิเคราะห์อัลกอริทึม] [ตารางไดนามิก] [ไบโนเมียลฮีพ] [เลซี่ไบโนเมียลฮีพ] [ฟิโบนักซี่ฮีพ] [สคริวฮีพ][รายการอ้างอิง]
![]()
ตารางไดนามิก
(Dynamic table)
ตารางไดนามิก คือ
ตารางจัดเก็บข้อมูลที่ขนาดของตารางสามารถขยายและยุบตัวได้ตามจำนวนข้อมูล
ถ้าในตารางนั้นมีการใส่ข้อมูลจนเต็มตาราง
การจะใส่ข้อมูลเข้าไปอีกจะต้องมีการสร้างตารางใหม่ที่มีขนาดใหญ่กว่าเดิม
และข้อมูลทั้งหมดที่ถูกจัดเก็บในตารางเดิม
ก็จะต้องถูกคัดลอกไปไว้ในตารางใหม่
ซึ่งเรียกว่า มีการขยายตาราง
ทำนองเดียวกันถ้าข้อมูลหลายๆตัวถูกลบออกจากตารางมากๆ
ก็จะต้องมีการสร้างตารางใหม่ที่มีขนาดเล็กลงกว่าเดิม
และข้อมูลทั้งหมดที่ถูกจัดเก็บในตารางเดิม
ก็จะต้องถูกคัดลอกไปไว้ในตารางใหม่
ซึ่งเรียกว่า มีการยุบตาราง
การขยายตาราง
เมื่อถึงจุดหนึ่งที่จะต้องมีการขยายตาราง
เช่นเมื่อช่องทั้งหมดในตารางมีข้อมูลเต็มอยู่
เป็นต้น
และต้องการเพิ่มข้อมูลลงไปอีก
ก็จะมีการสร้างตารางใหม่ที่มีขนาดใหญ่กว่าเดิม
พร้อมทั้งคัดลอกข้อมูลในตารางเดิมสู่ตารางใหม่
โดยทั่วไปการสร้างตารางใหม่จะสร้างให้มีขนาดเป็น
2 เท่าของตารางเดิม
| ให้ | T | เป็น ตาราง |
| table [T] | เป็น พอยเตอร์ที่จะชี้ไปยังตาราง | |
| num[T] | เป็น จำนวนข้อมูลในตาราง | |
| size[T] | เป็น จำนวนช่องข้อมูลทั้งหมดในตาราง |
สำหรับการวิเคราะห์ในแบบถัวเฉลี่ย
จะขอใช้วิธีศักย์ กำหนดให้ ![]() ที่จะมีค่าเริ่มต้นเป็น
0 และไม่มีค่าติดลบ
ที่จะมีค่าเริ่มต้นเป็น
0 และไม่มีค่าติดลบ ![]() = 2num[T] - size[T] ให้ Ci
เป็นต้นทุนจริงของการเพิ่มที่ i โดยที่ i
= 1, 2, ..., n
และให้การเพิ่มข้อมูล 1
ตัวลงในตารางใช้พลังงาน 1 หน่วย
= 2num[T] - size[T] ให้ Ci
เป็นต้นทุนจริงของการเพิ่มที่ i โดยที่ i
= 1, 2, ..., n
และให้การเพิ่มข้อมูล 1
ตัวลงในตารางใช้พลังงาน 1 หน่วย
การหาต้นทุนถัวเฉลี่ยของการเพิ่มข้อมูลลงในตารางไดนามิก
แบ่งได้เป็น 2 กรณี ดังนี้คือ
กรณีที่ 1
ถ้าการดำเนินงานการเพิ่มที่ i
ไม่ได้ส่งผลให้เกิดการขยายตาราง
sizei[T] = sizei-1-1[T]
และ
ต้นทุนถัวเฉลี่ยของการดำเนินงานจะเป็น
![]() = 1 + ( 2numi[T] - sizei[T] ) - (
2numi-1-1[T] - sizei-1-1[T]
)
= 1 + ( 2numi[T] - sizei[T] ) - (
2numi-1-1[T] - sizei-1-1[T]
)
= 1 + ( 2numi[T] - sizei[T] ) - ( 2( numi[T]
-1 ) - sizei[T] ) = 3
กรณีที่ 2
ถ้าการดำเนินงานการเพิ่มที่ i
ส่งผลให้เกิดการขยายตาราง sizei[T] / 2 =
sizei-1-1[T]
= numi[T] -1
และต้นทุนถัวเฉลี่ยของการดำเนินงาน
จะเป็น
![]() = numi[T] + ( 2numi[T]
- sizei[T] ) - ( 2numi-1-1[T] -
sizei-1-1[T] )
= numi[T] + ( 2numi[T]
- sizei[T] ) - ( 2numi-1-1[T] -
sizei-1-1[T] )
= numi[T] + ( 2numi[T]
- ( 2numi[T] -2 ) ) - ( 2( numi[T] + 1 ) - ( numi[T]
+ 1) ) = 3
นั่นคือ
ตารางจะมีการขยายหรือไม่ก็ตาม
ต้นทุนถัวเฉลี่ย
อย่างมากเท่ากับ 3 และจาก 2
กรณีข้างต้นสรุปว่า
ต้นทุนถัวเฉลี่ยต่อการเพิ่ม 1
ครั้งมีค่าคงที่
การยุบตาราง
ในการยุบตารางจะยุบเมื่อมีที่ว่างมากเกินไป
เช่นถ้ามีจำนวนข้อมูลน้อยกว่าเศษหนึ่งส่วนสี่ของจำนวนช่องข้อมูลทั้งหมดในตาราง
เป็นต้น
จะต้องมีการจัดหาตารางใหม่ให้มีขนาดเล็กลงกว่าเดิมครึ่งหนึ่งพร้อมทั้งคัดลอกข้อมูลจากตารางเก่าสู่ตารางใหม่
ส่วนตารางเก่าก็สามารถคืนให้กับระบบจัดการหน่วยความจำได้
สำหรับการวิเคราะห์ถัวเฉลี่ย
จะใช้วิธีศักย์เริ่มด้วยการนิยามฟังก์ชันศักย์
ที่จะมีค่าเริ่มต้นเป็น 0
และไม่มีค่าติดลบ ซึ่งก็คือ
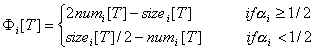
ให้ Ci
เป็นต้นทุนจริงของการแทรกที่ i โดยที่ i
= 1, 2, ..., n
และให้การลบข้อมูล 1
ตัวใช้พลังงาน 1 หน่วย
สำหรับการหาต้นทุนถัวเฉลี่ยของการลบข้อมูลในตารางไดนามิก
แบ่งได้เป็น 3 กรณี ดังนี้คือ
กรณีที่ 1
ถ้าการดำเนินงานการลบข้อมูลที่ i
ไม่ได้ส่งผลให้เกิดการยุบตาราง
โดยที่ ![]() i-1 < 1/2
ต้นทุนถัวเฉลี่ย เป็น
i-1 < 1/2
ต้นทุนถัวเฉลี่ย เป็น
![]() = 1 + ( sizei[T] / 2 - numi[T] ) - ( sizei-1[T] / 2 - numi-1[T] )
= 1 + ( sizei[T] / 2 - numi[T] ) - ( sizei-1[T] / 2 - numi-1[T] )
= 1 + ( sizei[T] / 2 - numi[T]
) - ( sizei[T] / 2 - (numi[T]+1) ) = 2
กรณีที่ 2
ถ้าการดำเนินงานการลบข้อมูลที่ i
ไม่ได้ส่งผลให้เกิดการยุบตาราง
โดยที่ ![]() i-1 > 1/2
ต้นทุนถัวเฉลี่ย เป็น
i-1 > 1/2
ต้นทุนถัวเฉลี่ย เป็น
![]() =
1 + ( 2numi[T] - sizei[T] ) - ( 2
numi-1[T] - sizei-1[T] )
=
1 + ( 2numi[T] - sizei[T] ) - ( 2
numi-1[T] - sizei-1[T] )
= 1 + ( 2numi[T] - sizei[T]
) - ( 2(numi[T] + 1) - sizei[T] ) = -1
หรือ
![]() = 1 + ( (sizei[T] / 2) - numi[T]
) - ( 2 numi-1[T] - sizei-1[T] )
= 1 + ( (sizei[T] / 2) - numi[T]
) - ( 2 numi-1[T] - sizei-1[T] )
= 1 + ( (numi[T]
+ 1) - numi[T]
) - ( 2(sizei-1[T] / 2) - sizei-1[T] ) = 1 + 1 = 2
กรณีที่ 3
ถ้าการดำเนินงานการลบข้อมูลที่ i
ส่งผลให้เกิดการยุบตาราง โดยที่
![]() i-1 < 1/2
ต้นทุนจริงของการดำเนินงานเป็น Ci = numi[T]
+1 เพราะว่า มีการลบข้อมูล 1 ตัว
และมีการย้ายข้อมูลจำนวน numi[T] ตัว โดยที่ sizei[T] / 2 =
sizei-11[T]
/ 4 = numi[T] +1
และต้นทุนถัวเฉลี่ยของการดำเนินงาน
จะเป็น
i-1 < 1/2
ต้นทุนจริงของการดำเนินงานเป็น Ci = numi[T]
+1 เพราะว่า มีการลบข้อมูล 1 ตัว
และมีการย้ายข้อมูลจำนวน numi[T] ตัว โดยที่ sizei[T] / 2 =
sizei-11[T]
/ 4 = numi[T] +1
และต้นทุนถัวเฉลี่ยของการดำเนินงาน
จะเป็น
![]() = (
numi[T]+1 ) + ( sizei[T] / 2 - numi[T]
) - ( sizei-1[T] / 2 - numi-1[T] )
= (
numi[T]+1 ) + ( sizei[T] / 2 - numi[T]
) - ( sizei-1[T] / 2 - numi-1[T] )
= ( numi[T]+1 ) + ( ( numi[T]+1
) - numi[T] ) - ( ( 2numi[T] + 2) - ( numi[T]+1
) ) = 1
จาก 3 กรณีข้างต้น สรุปว่าต้นทุนถัวเฉลี่ยต่อการลบ 1 ครั้ง มีค่าคงที่
สำหรับอัลกอริทึมการเพิ่มข้อมูลในตาราง และการลบข้อมูลในตารางเป็นดังนี้
| TABLE-INSERT(T,x) | ||
| 1. if size[T] = 0 | ||
| 2. | then allocate table[T] with 1 slot | |
| 3. | size[T] <-- 1 | |
| 4. if num[T] = size[T] | ||
| 5. | then allocate new-table with 2.size[T] slots | |
| 6. | insert all items in table[T] into new-table | |
| 7. | free table[T] | |
| 8. | table[T] <-- new-table | |
| 9. | size[T] <-- 2.size[T] | |
| 10. insert x into table[T] | ||
| 11. num[T] <-- num[T]+1 | ||
| TABLE-DELETE(T,x) | ||
| 1. delete x from table[T] | ||
| 2. num[T] <-- num[T] - 1 | ||
| 3. if num[T] = size[T] / 2 | ||
| 4. | then allocate new-table with size[T] / 2 slots | |
| 5. | insert all items in table[T] into new-table | |
| 6. | free table[T] | |
| 7. | table[T] <-- new-table | |
| 8. | size[T] <-- size[T] / 2 | |
การจินตทัศน์
| การจินตทัศน์การวิเคราะหถัวเฉลี่ย ในตารางไดนามิก |
![]()
[การวิเคราะห์อัลกอริทึม] [ตารางไดนามิก] [ไบโนเมียลฮีพ] [เลซี่ไบโนเมียลฮีพ] [ฟิโบนักซี่ฮีพ] [สคริวฮีพ][รายการอ้างอิง]